Error correction helps problem solving agents, even those which are limited in capability, to solve a much broader range of problems. This is particularly important as the Internet weighs towards finished artifacts (like books, posts, and articles) that have scant few examples of making an erroneous claim and then backtracking and fixing it. Can model problem solving performance improve if it was trained on examples of mistakes and their corrections? And how does this relate to the inherent difficulty of the problem in question?

To investigate this problem, I trained a toy maze-solving model that was allowed to backtrack on its prior moves. I found that the maze solving performance improved when errors and their corrections were injected into the paths of otherwise perfect solutions. I show that the probability of moving in the correct direction improves at decision points when mistakes are allowed.

This post also shows that, even though the training data teaches the model to make mistakes, this is outweighed by the benefits of backtracking, such that it learns to solve mazes more effectively.

I then investigated some of the world models in this fallible maze solving model. Future work could investigate the implications of this work for dataset filtering on problem-solving tasks, introducing synthetic errors and error corrections into existing datasets, and finding ways to lever down the mistake making intention.

Setup

I trained a small 10 million parameter transformer model to output solutions for square mazes between 3 and 9 tiles wide. At the core of the experiment, there were two datasets:

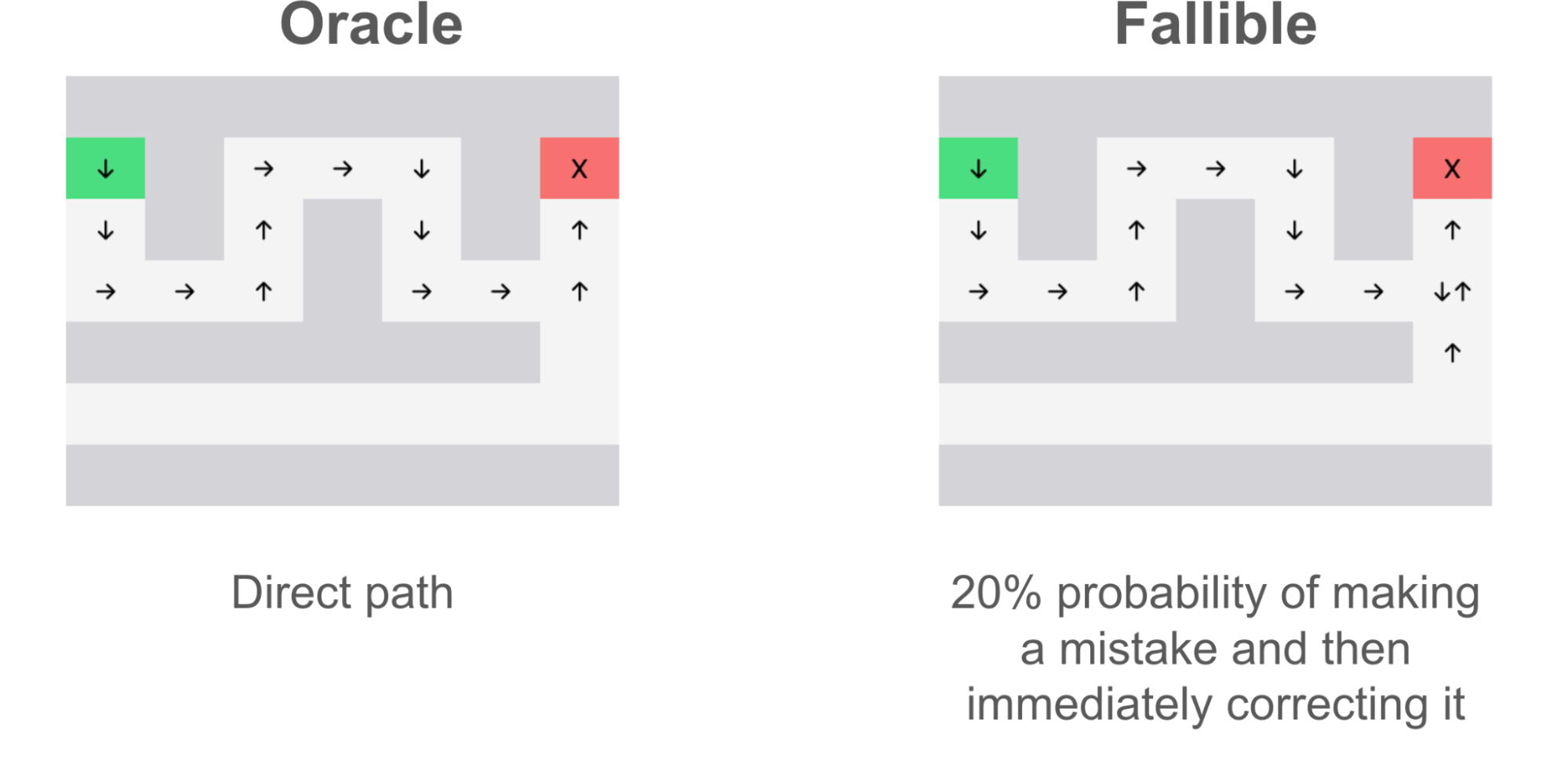
1. The oracle dataset, which unfailingly solves the maze every time in the shortest path.
2. The fallible dataset, which, like the oracle, goes directly to the end. However, at every junction point, there is a 20% chance of making the wrong decision. Each time it makes the wrong decision, it immediately backtracks and continues on the path.

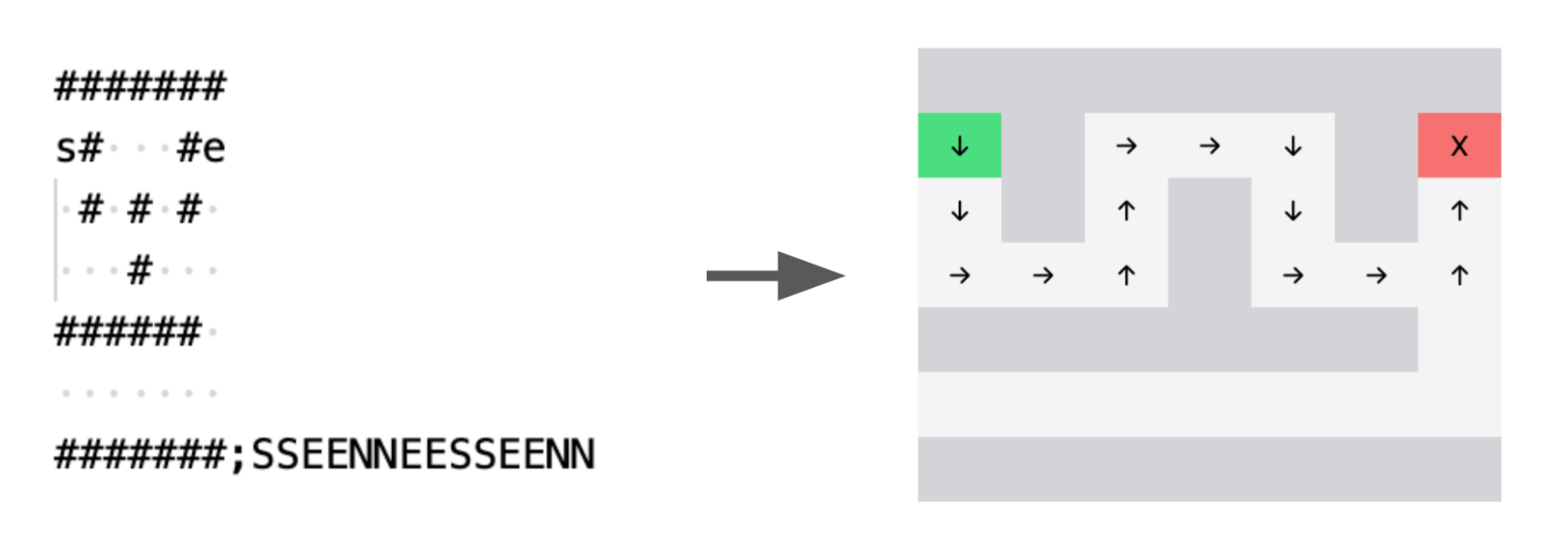
I serialized mazes with a pretty simple scheme, without doing anything fancier (like serializing with a space filling curve, or serializing spans as in this paper, which I found unnecessary):

Performance

Behavior on decision points

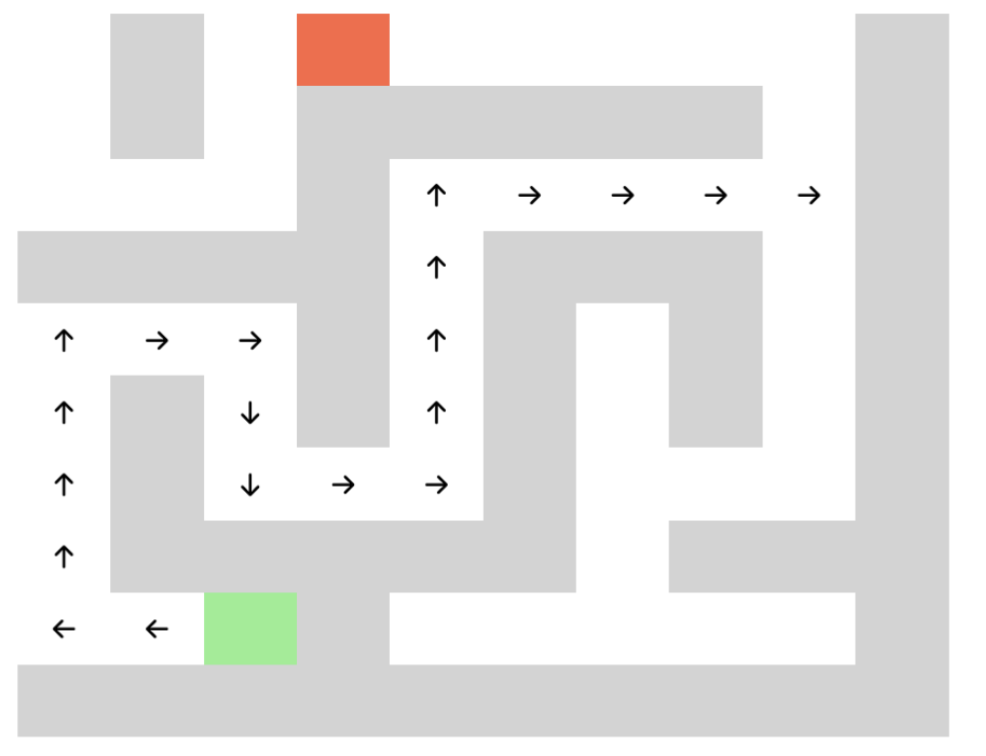
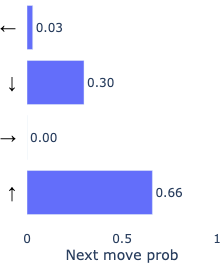
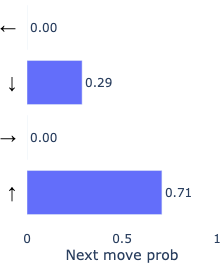
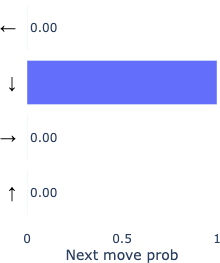
Let’s look at model behavior by investigating a point where both models were not confident about which direction was next. As a case study to prime intuition, at this decision point, both models were ~70% confident in the directly correct move, and we can analyze what happens in the other ~30% of the time.

Board state	Next move predictions
	Oracle model	Fallible model
Decision point
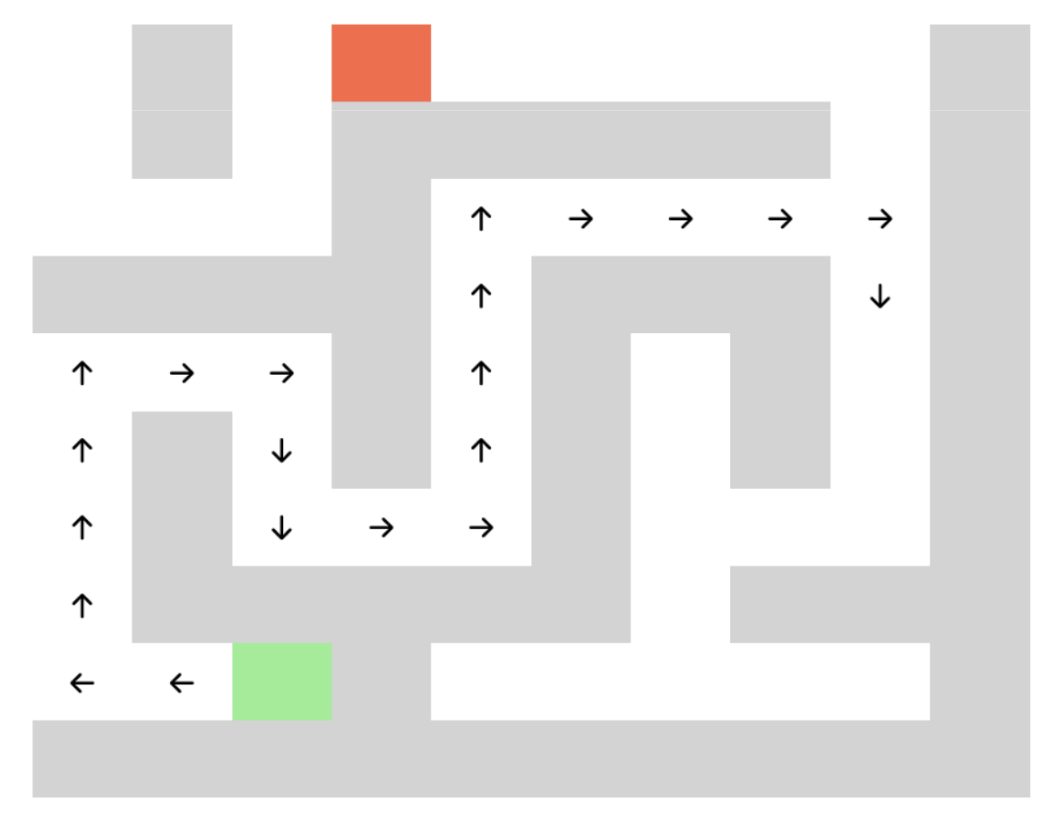
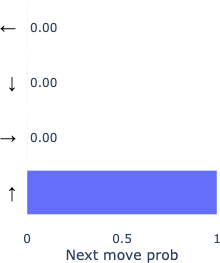
After making a mistake

Because our metric for correctness does not penalize backtracking, we can see here that the fallible model actually goes on to determine the correct backtracking move, while the oracle model remains confident in moving forward. This example (though rather weak evidence) suggests the model not only learns to effectively backtrack when it’s wrong, but also by implication learns to judge from its current inferred position as to whether or not it’s on the wrong path. Another reasonable interpretation is that it uses an extra move to “think” more about the move, being afforded extra computation.

Benchmark performance

It might not be obvious why a model trained on the fallible dataset would perform better at solving mazes, because while it learns to correct its errors, it also learns to make mistakes as well. It seems plausible that these two effects would cancel out, and you’d have a model no better (or even slightly worse) than the oracle model.

To test this, I constructed a benchmark where both models generated solutions for 2000 mazes, which were then checked for correctness. A solution was correct if it got to the end and didn’t cheat by going through any walls.

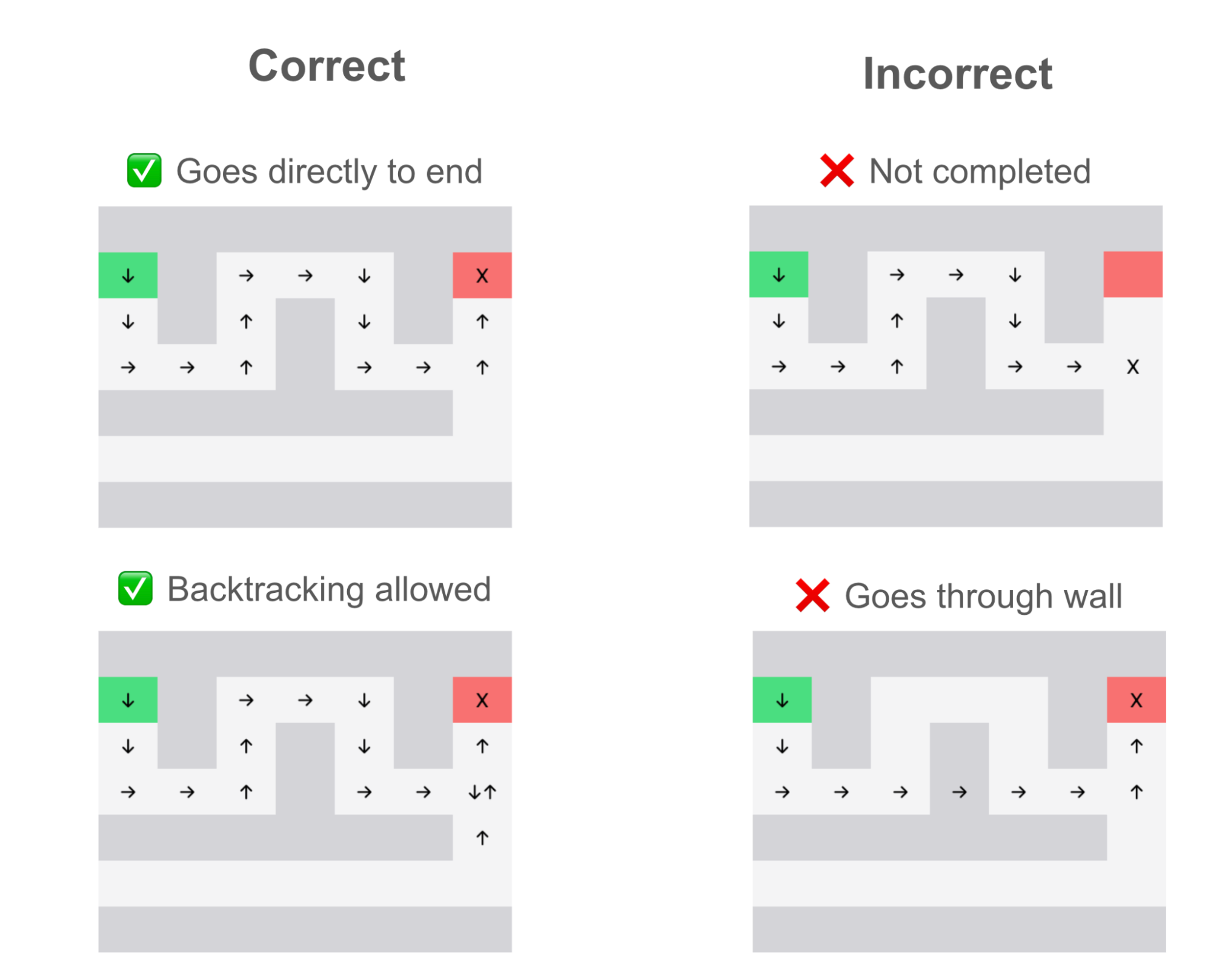
Running this benchmark on multiple pairs of models at various different sizes reveals that the fallible model performs better than the oracle model at every size tested, despite being otherwise identical. This difference is fairly tangible, improving maze solving performance between 2% and 5%.

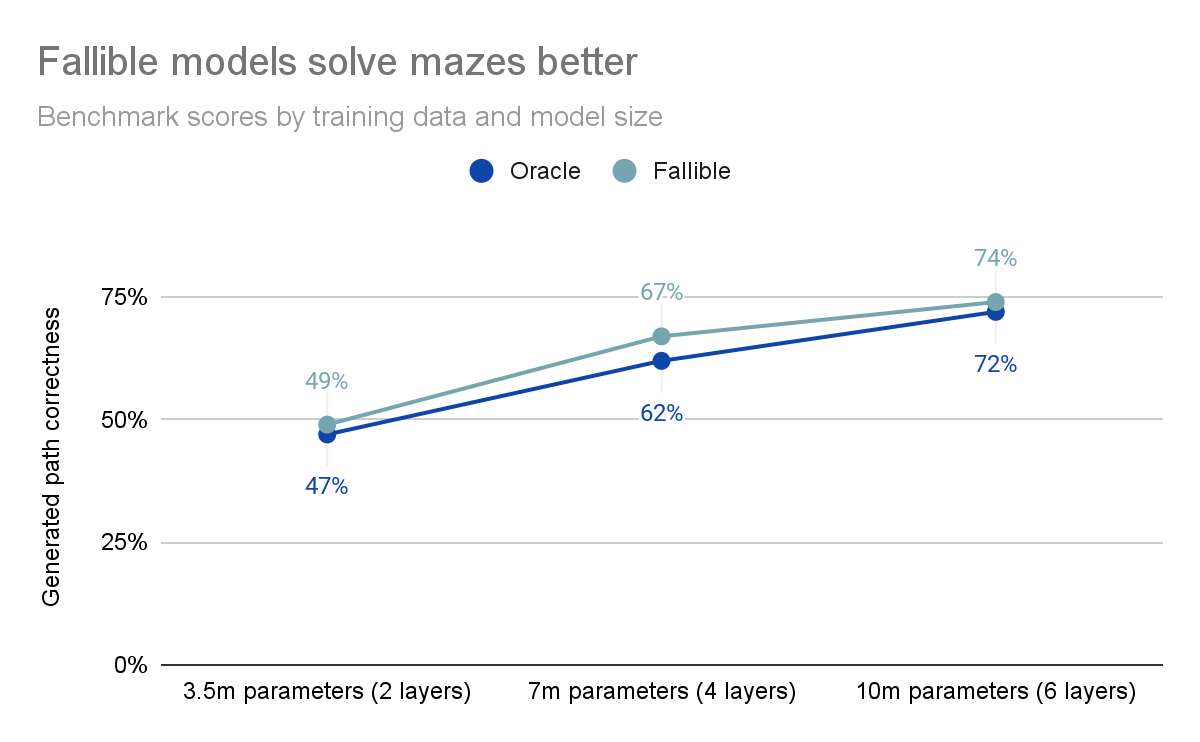
This indicates that the fallible model has a consistent performance advantage , even though you could imagine many reasons this should not be true (the generated paths are longer and more confusing, the training data moves are occasionally going the wrong way and so the objective signal is more noisy, etc). I find this result quite surprising as the fallible model has a distinct decision-making disadvantage, since it is trained to make mistakes.

Probing the residual stream

I thought it was interesting to try to probe the residual stream to see how it understood mazes, and in particular if it represented mistaken moves.

It’s interesting that I couldn’t find a linear representation of mistaken moves in the residual stream. I trained a linear probe that couldn’t pick it up, but a non-linear probe with a simple ReLu could pick it up easily. A similar parallel happened in investigating OrthelloGPT, where it turned out that the model learned a feature for “my move vs. your move” instead of “black move vs white move”. It’s plausible something similar is true of this case as well.

I would bet that there is some actual representation of what a mistake is linearly, but maybe the definition I’m using is slightly wrong, or the training process process is too sensitive. I’m super curious to see what this model could actually be learning and how this differs from human intuition.

The non-linear probe reveals something about how the model decides where to go. In the figure below, we take partially completed paths and move around the endpoint of the maze, plotting the value of the mistake feature as we go. As the endpoint is moved behind the path, the mistake feature is more activated, versus when it is in front of the current position:

Another technique to try would have been to use a sparse autoencoder, but these seem to have problems of their own.

Next steps

• I still find it pretty interesting that using an extra token, in this case a wrong move, actually improves the overall performance. Can the same effect be observed by other means, for instance, outputting an empty token so more computation can be performed?
• Can this be generalized to non-turn-based problem solving, like writing an English essay, where there are no concrete “moves”? This probably requires more understanding of how models think and how to wield the tools of mechanistic interpretability more effectively.
• Can mathematical reasoning be improved this way? This sort of marking of incorrect and incorrect moves is currently pretty constrained to problems solved through discrete moves. Mathematical reasoning seems like a particularly good candidate for this intervention!